Robust numerical method for a system of singularly perturbed parabolic reaction‐diffusion equations on a rectangle

Abstract

A Dirichlet problem is considered for a system of two singularly perturbed parabolic reaction‐diffusion equations on a rectangle. The parabolic boundary layer appears in the solution of the problem as the perturbation parameter ϵ tends to zero. On the basis of the decomposition solution technique, estimates for the solution and derivatives are obtained. Using the condensing mesh technique and the classical finite difference approximations of the boundary value problem under consideration, a difference scheme is constructed that converges ϵ‐uniformly at the rate 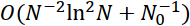 , where 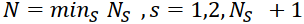and N₀ + 1 are the numbers of mesh points on the axis x_s and on the axis t, respectively.

First Published Online: 14 Oct 2010