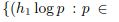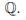A discrete version of the Mishou theorem related to periodic zeta-functions
DOI: https://doi.org/10.3846/mma.2024.19502Abstract
In the paper, we consider simultaneous approximation of a pair of analytic functions by discrete shifts 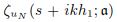
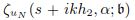
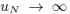
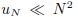
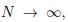
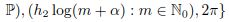
Keywords:
Mishou theorem, periodic zeta-function, periodic Hurwitz zeta-function, universalityHow to Cite
Share
License
Copyright (c) 2024 The Author(s). Published by Vilnius Gediminas Technical University.

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
B. Bagchi. The Statistical Behaviour and Universality Properties of the Riemann Zeta-Function and Other Allied Dirichlet Series. PhD Thesis, Indian Statistical Institute, Calcutta, 1981.
A. Balčiūnas, A. Dubickas and A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Mathematical Notes, 105(1):173–179, 2019. https://doi.org/10.1134/S0001434619010218"> https://doi.org/10.1134/S0001434619010218
A. Balčiūnas, V. Garbaliauskienė, V. Lukšienė, R. Macaitienė and A. Rimkevičienė. Joint discrete approximation of analytic functions by Hurwitz zeta-functions. Mathematical Modelling and Analysis, 27(1):88–100, 2022. https://doi.org/10.3846/mma.2022.15068"> https://doi.org/10.3846/mma.2022.15068
A. Balčiūnas, M. Jasas, R. Macaitienė and D. Šiaučiūnas. On the Mishou theorem for zeta-functions with periodic coefficients. Mathematics, 11(9):2042, 2023. https://doi.org/10.3390/math11092042"> https://doi.org/10.3390/math11092042
A. Balčiūnas, A. Laurinčikas and M. Stoncelis. On a Dirichlet series connected to a periodic Hurwitz zeta-function with transcendental and rational parameter. Mathematical Modelling and Analysis, 28(1):91–101, 2023. https://doi.org/10.3846/mma.2023.17222"> https://doi.org/10.3846/mma.2023.17222
E. Buivydas and A. Laurinčikas. A discrete version of the Mishou theorem. The Ramanujan Journal, 38(2):331–347, 2015. https://doi.org/10.1007/s11139-014-9631-2"> https://doi.org/10.1007/s11139-014-9631-2
E. Buivydas and A. Laurinčikas. A generalized joint discrete universality theorem for the Riemann and Hurwitz zeta-functions. Lithuanian Mathematical Journal, 55(2):193–206, 2015. https://doi.org/10.1007/s10986-015-9273-0"> https://doi.org/10.1007/s10986-015-9273-0
V. Franckevič, A. Laurinčikas and D. Šiaučiūnas. On approximation of analytic functions by periodic Hurwitz zeta-functions. Mathematical Modelling and Analysis, 24(1):20–33, 2019. https://doi.org/10.3846/mma.2019.002"> https://doi.org/10.3846/mma.2019.002
M. Jasas, A. Laurinčikas and D. Šiaučiūnas. On the approximation of analytic functions by shifts of absolutely convergent Dirichlet series. Mathematical Notes, 109(5):876–883, 2021. https://doi.org/10.1134/S0001434621050217"> https://doi.org/10.1134/S0001434621050217
M. Jasas, A. Laurinčikas, M. Stoncelis and D. Šiaučiūnas. Discrete universality of absolutely convergent Dirichlet series. Mathematical Modelling and Analysis, 27(1):78–87, 2022. https://doi.org/10.3846/mma.2022.15069"> https://doi.org/10.3846/mma.2022.15069
A. Javtokas and A. Laurinčikas. Universality of the periodic Hurwitz zetafunction. Integral Transforms and Special Functions, 17(10):711–722, 2006. https://doi.org/10.1080/10652460600856484"> https://doi.org/10.1080/10652460600856484
R. Kačinskaitė and A. Laurinčikas. The joint distribution of periodic zetafunctions. Studia Scientiarum Mathematicarum Hungarica, 48(2):257–279, 2011. https://doi.org/10.1556/sscmath.48.2011.2.1162"> https://doi.org/10.1556/sscmath.48.2011.2.1162
A. Laurinčikas. The joint discrete universality of periodic zeta-functions. In J. Sander, J. Steuding and R. Steuding(Eds.), From Arithmetic to ZetaFunctions, Number Theory in Memory of Wolfgang Schwarz, pp. 231–246. Springer, 2016. https://doi.org/10.1007/978-3-319-28203-9_15"> https://doi.org/10.1007/978-3-319-28203-9_15
A. Laurinčikas. A discrete version of the Mishou theorem. II. Proceedings of the Steklov Institute of Mathematics, 296(1):172–182, 2017. https://doi.org/10.1134/S008154381701014X"> https://doi.org/10.1134/S008154381701014X
A. Laurinčikas. On discrete universality of the Hurwitz zeta-function. Results in Mathematics, 72(1):907–917, 2017. https://doi.org/10.1007/s00025-017-0702-8"> https://doi.org/10.1007/s00025-017-0702-8
A. Laurinčikas. Discrete universality of the Riemann zeta-function and uniform distribution modulo 1. St. Petersburg Mathematical Journal, 30:103–110, 2019. https://doi.org/10.1090/spmj/1532"> https://doi.org/10.1090/spmj/1532
A. Laurinčikas. On the Mishou theorem with algebraic parameter. Siberian Mathematical Journal, 60(6):1075–1082, 2019. https://doi.org/10.1134/S0037446619060144"> https://doi.org/10.1134/S0037446619060144
A. Laurinčikas. Universality of the Riemann zeta-function in short intervals. Journal of Number Theory, 204:279–295, 2019. https://doi.org/10.1016/j.jnt.2019.04.006"> https://doi.org/10.1016/j.jnt.2019.04.006
A. Laurinčikas. Discrete universality of the Riemann zeta-function in short intervals. Applicable Analysis and Discrete Mathematics, 14(2):382–405, 2020. https://doi.org/10.2298/AADM190704019L"> https://doi.org/10.2298/AADM190704019L
A. Laurinčikas. Approximation by generalized shifts of the Riemann zetafunction in short intervals. The Ramanujan Journal, 56(1):309–322, 2021. https://doi.org/10.1007/s11139-021-00405-y"> https://doi.org/10.1007/s11139-021-00405-y
A. Laurinčikas. Approximation of analytic functions by an absolutely convergent Dirichlet series. Archiv der Mathematik, 117(1):53–63, 2021. https://doi.org/10.1007/s00013-021-01616-x"> https://doi.org/10.1007/s00013-021-01616-x
A. Laurinčikas. On the universality of the Riemann and Hurwitz zeta-functions. Results in Mathematics, 77(1):29, 2021. https://doi.org/10.1007/s00025-021-01564-6"> https://doi.org/10.1007/s00025-021-01564-6
A. Laurinčikas. The universality of absolutely covergent series on short intervals. Siberian Mathematical Journal, 62(6):1076–1083, 2021. https://doi.org/10.1134/S0037446621060094"> https://doi.org/10.1134/S0037446621060094
A. Laurinčikas. On joint universality of the Riemann and Hurwitz zeta-functions. Mathematical Notes, 111(3):571–578, 2022. https://doi.org/10.1134/S0001434622030257"> https://doi.org/10.1134/S0001434622030257
A. Laurinčikas. On the universality of the zeta functions of certain cusp forms. Sbornik: Mathematics, 213(5):659–670, 2022. https://doi.org/10.1070/SM9650"> https://doi.org/10.1070/SM9650
A. Laurinčikas. New aspects of universality of Hurwitz zeta-functions. Analysis Mathematica, 49(1):183–193, 2023. https://doi.org/10.1007/s10476-023-0188-4"> https://doi.org/10.1007/s10476-023-0188-4
A. Laurinčikas and R. Garunkštis. The Lerch Zeta-Function. Kluwer Academic Publishers, Dordrecht, Boston, London, 2002.
A. Laurinčikas, R. Macaitienė, D. Mochov and D. Šiaučiūnas. Universality of the periodic Hurwitz zeta-function with rational parameter. Siberian Mathematical Journal, 59(5):894–900, 2018. https://doi.org/10.1134/S0037446618050130"> https://doi.org/10.1134/S0037446618050130
A. Laurinčikas, R. Macaitienė and D. Šiaučiūnas. A generalization of the Voronin theorem. Lithuanian Mathematical Journal, 59(2):156–168, 2019. https://doi.org/10.1007/s10986-019-09418-z"> https://doi.org/10.1007/s10986-019-09418-z
A. Laurinčikas, R. Macaitienė and D. Šiaučiūnas. Universality of an absolutely convergent Dirichlet series with modified shifts. Turkish Journal of Mathematics, 46(6):2440–2449, 2022. https://doi.org/10.55730/1300-0098.3279"> https://doi.org/10.55730/1300-0098.3279
A. Laurinčikas and D. Šiaučiūnas. Remarks on the universality of the periodic zeta-function. Mathematical Notes, 80(3):532–538, 2006. https://doi.org/10.1007/s11006-006-0171-y"> https://doi.org/10.1007/s11006-006-0171-y
A. Laurinčikas and D. Šiaučiūnas. Discrete approximation by Dirichlet series connected to the Riemann zeta-function. Mathematics, 9(10):1073, 2021. https://doi.org/10.3390/math9101073"> https://doi.org/10.3390/math9101073
A. Laurinčikas, D. Šiaučiūnas and G. Vadeikis. Weighted discrete universality of the Riemann zeta-function. Mathematical Modelling and Analysis, 25(1):21–36, 2020. https://doi.org/10.3846/mma.2020.10436"> https://doi.org/10.3846/mma.2020.10436
A. Laurinčikas, D. Šiaučiūnas and G. Vadeikis. A weighted version of the Mishou theorem. Mathematical Modelling and Analysis, 26(1):21–33, 2021. https://doi.org/10.3846/mma.2021.12445"> https://doi.org/10.3846/mma.2021.12445
H. Mishou. The joint value-distribution of the Riemann zeta function and Hurwitz zeta functions. Lithuanian Mathematical Journal, 47(1):32–47, 2007. https://doi.org/10.1007/s10986-007-0003-0"> https://doi.org/10.1007/s10986-007-0003-0
Yu.V. Nesterenko. Modular functions and transcendence questions. Sbornik: Mathematics, 187(9):1319–1348, 1996. https://doi.org/10.1070/sm1996v187n09abeh000158"> https://doi.org/10.1070/sm1996v187n09abeh000158
A. Reich. Werteverteilung von Zetafunktionen. Archiv der Mathematik, 34(1):440–451, 1980. https://doi.org/10.1007/BF01224983"> https://doi.org/10.1007/BF01224983
A. Sourmelidis and J. Steuding. On the value distribution of Hurwitz zetafunctions with algebraic parameter. Constructive Approximation, 55(3):829–860, 2022. https://doi.org/10.1007/s00365-021-09561-2"> https://doi.org/10.1007/s00365-021-09561-2
S.M. Voronin. Theorem on the “universality” of the Riemann zeta-function. Izv. Akad. Nauk SSSR, Ser. Matem., 39:475–486, 1975. (in Russian)
View article in other formats
Published
Issue
Section
Copyright
Copyright (c) 2024 The Author(s). Published by Vilnius Gediminas Technical University.
License

This work is licensed under a Creative Commons Attribution 4.0 International License.