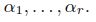Joint discrete approximation of analytic functions by Hurwitz zeta-functions
DOI: https://doi.org/10.3846/mma.2022.15068Abstract
Let H(D) be the space of analytic functions on the strip . In this paper, it is proved that there exists a closed non-empty set
such that every collection of the functions
is approximated by discrete shifts
, of Hurwitz zeta-functions with arbitrary parameters
Keywords:
Hurwitz zeta-function, space of analytic functions, weak convergence, universalityHow to Cite
Share
License
Copyright (c) 2022 The Author(s). Published by Vilnius Gediminas Technical University.

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
B. Bagchi. The Statistical Behaviuor and Universality Properties of the Riemann Zeta-Function and Other Allied Dirichlet Series. PhD Thesis, Indian Statistical Institute, Calcutta, 1981.
A. Balčiūnas, A. Dubickas and A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Math. Notes, 105(1-2):173–179, 2019. https://doi.org/10.1134/S0001434619010218"> https://doi.org/10.1134/S0001434619010218
A. Balčiūnas, V. Garbaliauskienė, J. Karaliūnaitė, R. Macaitienė, J. Petuškinaitė and A. Rimkevičienė. Joint discrete approximation of a pair of analytic functions by periodic zeta-functions. Math. Modell. Analysis, 25(1):71–87, 2020. https://doi.org/10.3846/mma.2020.10450"> https://doi.org/10.3846/mma.2020.10450
P. Billingsley. Convergence of Probability Measures. Willey, New York, 1968.
E. Buivydas and A. Laurinčikas. A discrete version of the Mishou theorem. RamanujanJ., 38(2):331–347, 2015. https://doi.org/10.1007/s11139-014-9631-2"> https://doi.org/10.1007/s11139-014-9631-2
E. Buivydas and A. Laurinčikas. A generalized joint discrete universality theorem for the Riemann and Hurwitz zeta-functions. Lith. Math. J., 55(2):193–206, 2015. https://doi.org/10.1007/s10986-015-9273-0"> https://doi.org/10.1007/s10986-015-9273-0
E. Buivydas, A. Laurinčikas, R. Macaitienė and J. Rašytė. Discrete universality theorems for the Hurwitz zeta-function. J. Approx. Th., 183:1–13, 2014. https://doi.org/10.1016/j.jat.2014.03.006"> https://doi.org/10.1016/j.jat.2014.03.006
V. Franckeviče, A. Laurinčikas and D. Šiaučiūnas. On joint value distribution of Hurwitz zeta-functions. Chebyshevskii Sb., 19(3):219–230, 2018.
V. Franckevič, A. Laurinčikas and D. Šiaučiūnas. On approximation of analytic functions by periodic Hurwitz zeta-functions. Math. Modell. Analysis, 24(1):20– 33, 2019. https://doi.org/10.3846/mma.2019.002"> https://doi.org/10.3846/mma.2019.002
S.M. Gonek. Analytic Properties of Zeta and L-Functions. PhD Thesis, University of Michigan, 1979.
A. Javtokas and A. Laurinčikas. Universality of the periodic Hurwitz zeta-function. Integral Transforms Spec. Funct., 17(10):711–722, 2006. https://doi.org/10.1080/10652460600856484"> https://doi.org/10.1080/10652460600856484
R. Kačinskaitė and A. Laurinčikas. The joint distribution of periodic zeta-functions. Studia Sci. Math. Hungar., 48(2):257–279, 2011. https://doi.org/10.1556/sscmath.48.2011.2.1162"> https://doi.org/10.1556/sscmath.48.2011.2.1162
A. Laurinčikas. The joint universality of Hurwitz zeta-functions. Siauliai Math. Semin., 3 (11):169–187, 2008.
A. Laurinčikas. Joint universality of zeta-functions with periodic coefficients. Izv. Math., 74(3):515–539, 2010. https://doi.org/10.1070/IM2010v074n03ABEH002497"> https://doi.org/10.1070/IM2010v074n03ABEH002497
A. Laurinčikas. A discrete universality theorem for the Hurwitz zeta-function. J. Number Th., 143:232–247, 2014. https://doi.org/10.1016/j.jnt.2014.04.013"> https://doi.org/10.1016/j.jnt.2014.04.013
A. Laurinčikas. Distribution modulo 1 and universality of the Hurwitz zeta-function. J. Number Th., 167:294–303, 2016. https://doi.org/10.1016/j.jnt.2016.03.013"> https://doi.org/10.1016/j.jnt.2016.03.013
A. Laurinčikas. Universality theorems for zeta-functions with periodic coefficients. Siber. Math. J., 57(2):330–339, 2016. https://doi.org/10.1134/S0037446616020154"> https://doi.org/10.1134/S0037446616020154
A. Laurinčikas. A discrete version of the Mishou theorem. II. Proc. Steklov Inst. Math., 296(1):172–182, 2017. https://doi.org/10.1134/S008154381701014X"> https://doi.org/10.1134/S008154381701014X
A. Laurinčikas. On discrete universality of the Hurwitz zeta-function. Results Math., 72(1-2):907–917, 2017. https://doi.org/10.1007/s00025-017-0702-8"> https://doi.org/10.1007/s00025-017-0702-8
A. Laurinčikas. Joint value distribution theorems for the Riemann and Hurwitz zeta-functions. Moscow Math. J., 18(2):349–366, 2018. https://doi.org/10.17323/1609-4514-2018-18-2-349-366"> https://doi.org/10.17323/1609-4514-2018-18-2-349-366
A. Laurinčikas. “Almost” universality of the Lerch zeta-function. Math. Commun., 24(1):107–118, 2019.
A. Laurinčikas. Joint discrete universality for periodic zeta-functions. Quaest. Math., 42(5):687–699, 2019. https://doi.org/10.2989/16073606.2018.1481891"> https://doi.org/10.2989/16073606.2018.1481891
A. Laurinčikas. Non-trivial zeros of the Riemann zeta-function and joint universality theorems. J. Math. Anal. Appl., 475(1):385–402, 2019. https://doi.org/10.1016/j.jmaa.2019.02.047"> https://doi.org/10.1016/j.jmaa.2019.02.047
A. Laurinčikas. On the Mishou theorem with algebraic parameter. Siber. Math. J., 60(6):1075–1082, 2019. https://doi.org/10.1134/S0037446619060144"> https://doi.org/10.1134/S0037446619060144
A. Laurinčikas. Joint discrete universality for periodic zeta-functions. II. Quaest. Math., 43(12):1765–1779, 2020. https://doi.org/10.2989/16073606.2019.1654554"> https://doi.org/10.2989/16073606.2019.1654554
A. Laurinčikas. Zeros of the Riemann zeta-function in the discrete universality of the Hurwitz zeta-function. Studia Sci. Math. Hungar., 57(2):147–164, 2020. https://doi.org/10.1556/012.2020.57.2.1460"> https://doi.org/10.1556/012.2020.57.2.1460
A. Laurinčikas. On the Hurwitz zeta-function with algebraic irrational parameter. Proc. Steklov Inst. Math., http://mi.mathnet.ru/tm4165"> http://mi.mathnet.ru/tm4165
A. Laurinčikas and R. Garunkštis. The Lerch Zeta-Function. Kluwer Academic Publishers, Dordrecht, Boston, London, 2002.
A. Laurinčikas and R. Macaitienė. The discrete universality of the periodic Hurwitz zeta function. Integral Transforms Spec. Funct., 20(9-10):673–686, 2009. https://doi.org/10.1080/10652460902742788"> https://doi.org/10.1080/10652460902742788
A. Laurinčikas and R. Macaitienė. Joint approximation of analytic functions by shifts of the Riemann and periodic Hurwitz zeta-functions. Appl. Anal. Discrete Math., 12(2):508–527, 2018. https://doi.org/10.2298/AADM170713016L"> https://doi.org/10.2298/AADM170713016L
A. Laurinčikas, R. Macaitienė, D. Mochov and D. Šiaučiūnas. Universality of the periodic Hurwitz zeta-function with rational parameter. Sib. Math. J., 59(5):894–900, 2018. https://doi.org/10.1134/S0037446618050130"> https://doi.org/10.1134/S0037446618050130
R. Macaitienė and D. Šiaučiūnas. Joint universality of Hurwitz zeta-functions and nontrivial zeros of the Riemann zeta-function. Lith. Math. J., 59(1):81–95, 2019. https://doi.org/10.1007/s10986-019-09423-2"> https://doi.org/10.1007/s10986-019-09423-2
H. Mishou. The joint value distribution of the Rieman zeta-function and Hurwitz zeta-functions. Lith. Math. J., 47(1):32–47, 2007. https://doi.org/10.1007/s10986-007-0003-0"> https://doi.org/10.1007/s10986-007-0003-0
H.L. Montgomery. Topics in Multiplicative Number Theory. Lecture Notes Math. Vol. 227, Springer-Verlag, Berlin, 1971. https://doi.org/10.1007/BFb0060851"> https://doi.org/10.1007/BFb0060851
J. Sander and J. Steuding. Joint universality for sums and products of Dirichlet L-functions. Analysis (Munich), 26(3):295–312, 2006. https://doi.org/10.1524/anly.2006.26.99.295"> https://doi.org/10.1524/anly.2006.26.99.295
S.M. Voronin. Analytic Properties of Generating Function of Arithmetic Objects. Diss. doktor fiz.-matem. nauk, Steklov Math. Inst., Moscow, 1977 (in Russian).
View article in other formats
Published
Issue
Section
Copyright
Copyright (c) 2022 The Author(s). Published by Vilnius Gediminas Technical University.
License

This work is licensed under a Creative Commons Attribution 4.0 International License.