Joint discrete approximation of analytic functions by shifts of Lerch zeta-functions
DOI: https://doi.org/10.3846/mma.2024.19493Abstract
The Lerch zeta-function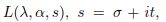 
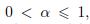
depends on two real parameters λ and 
and, for σ > 1, is defined by the Dirichlet series 
, and by analytic continuation elsewhere. In the paper, we consider the joint approximation of collections of analytic functions by discrete shifts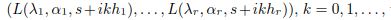 
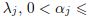
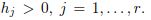
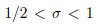
with arbitrary 
1 and 
We prove that there exists a non-empty closed set of analytic functions on the critical strip 
which is approximated by the above shifts. It is proved that the set of shifts approximating a given collection of analytic functions has a positive lower density. The case of positive density also is discussed. A generalization for some compositions is given.
Keywords:
approximation of analytic functions, Lerch zeta-functions, space of analytic functions, weak convergence of probability measuresHow to Cite
Share
License
Copyright (c) 2024 The Author(s). Published by Vilnius Gediminas Technical University.
This work is licensed under a Creative Commons Attribution 4.0 International License.
References
T.M. Apostol. On the Lerch zeta function. Pacific J. Math., 1:161–167, 1951.
T.M. Apostol. Addendum to “On the Lerch zeta function”. Pacific J. Math., 2:10, 1952.
B. Bagchi. The Statistical Behaviour and Universality Properties of the Riemann Zeta-Function and Other Allied Dirichlet Series. PhD Thesis, Indian Statistical Institute, Calcutta, 1981.
A. Balčiūnas, V. Garbaliauskienė, V. Lukšienė, R. Macaitienė and A. Rimkevičienė. Joint discrete approximation of analytic functions by Hurwitz zeta-functions. Math. Modell. Anal., 27(1):88–100, 2002. https://doi.org/10.3846/mma.2022.15068"> https://doi.org/10.3846/mma.2022.15068
B.C. Berndt. Two new proofs of Lerch’s functional equation. Proc. Amer. Math. Soc., 32:403–408, 1972.
P. Billingsley. Convergence of Probability Measures. 2nd eition, Wiley, New York, 1999. https://doi.org/10.1002/9780470316962"> https://doi.org/10.1002/9780470316962
R. Garunkštis. The universality theorem with weight for the Lerch zeta-function. In A. Laurinčikas, E. Manstavičius and V. Stakėnas(Eds.), Analytic and Probabilistic Methods in Number Theory, Proceedings of the Second Intern. Conf. in Honour of J. Kubilius, Palanga, Lithuania, 23-27 September 1996, pp. 59–67, Vilnius, Utrecht, 1997. TEV, VSP. https://doi.org/10.1515/9783110944648.59"> https://doi.org/10.1515/9783110944648.59
S.M. Gonek. Analytic Properties of Zeta and L-Functions. PhD Thesis, University of Michigan, 1979. https://doi.org/10.7302/11403"> https://doi.org/10.7302/11403
A. Hurwitz. Einige Eigenschaften der Dirichletschen Funktionen F(s) = ∑(D/n)n/1s, die bei der Bestimmung der Klassenanzahlen binärer quadratischer Formen auftreten. Zeitschrift Math. Phys., 27:86–101, 1882.
A.A. Karatsuba and S.M. Voronin. The Riemann Zeta-Function. Walter de Gruyter, Berlin, 1992. https://doi.org/10.1515/9783110886146"> https://doi.org/10.1515/9783110886146
R. Kačinskaitė and K. Matsumoto. On mixed discrete universality for a class of zeta-functions: a further generalization. Math. Modell. Anal., 25(4):569–583, 2020. https://doi.org/10.3846/mma.2020.11751"> https://doi.org/10.3846/mma.2020.11751
A. Laurinčikas. Limit Theorems for the Riemann Zeta-Function. Kluwer, Dordrecht, 1996. https://doi.org/10.1007/978-94-017-2091-5"> https://doi.org/10.1007/978-94-017-2091-5
A. Laurinčikas. The universality of the Lerch zeta-function. Lith. Math. J., 37(3):275–280, 1997.
A. Laurinčikas. “Almost” universality of the Lerch zeta-function. Math. Commun., 24(1):107–118, 2019.
A. Laurinčikas and R. Garunkštis. The Lerch Zeta-Function. Kluwer Academic Publishers, Dordrecht, Boston, London, 2002. https://doi.org/10.1007/978-94-017-6401-8"> https://doi.org/10.1007/978-94-017-6401-8
A. Laurinčikas and R. Macaitienė. The discrete universality of the periodic Hurwitz zeta function. Integral Transforms Spec. Funct., 20(9-10):673–686, 2009. https://doi.org/10.1080/10652460902742788"> https://doi.org/10.1080/10652460902742788
A. Laurinčikas and K. Matsumoto. The joint universality and the functional independence for Lerch zeta-functions. Nagoya Math. J., 157:211–227, 2000. https://doi.org/10.1017/S002776300000725X"> https://doi.org/10.1017/S002776300000725X
A. Laurinčikas and K. Matsumoto. Joint value distribution theorems on Lerch zeta-functions. III. In A. Laurinčikas and E. Manstavičius(Eds.), Analytic and Probabilistic Methods in Number Theory, pp. 87–98, Vilnius, 2007. TEV.
A. Laurinčikas and A. Mincevič. Joint discrete universality for Lerch zeta-functions. Chebyshevskii Sbornik, 19(1):138–151, 2018.
A. Laurinčikas, T. Mikalauskaitė and D. Šiaučiūnas. Joint approximation of analytic functions by shifts of Lerch zeta-functions. Mathematics, 11(3):752, 2023. https://doi.org/10.3390/math11030752"> https://doi.org/10.3390/math11030752
Y. Lee, T. Nakamura and L . Pańkowski. Joint universality for Lerch zeta-function. J. Math. Soc. Japan, 69(1):153–168, 2017. https://doi.org/10.48550/arXiv.1503.06001"> https://doi.org/10.48550/arXiv.1503.06001
M. Lerch. Note sur la fonction k(w, x, s) = ∑n⩾0 exp{2πinx}(n + w)−s. Acta Math., 11:19–24, 1887.
K. Matsumoto. A survey on the theory of universality for zeta and L-functions. In M. Kaneko, S. Kanemitsu and J. Liu(Eds.), Number Theory: Plowing and Starring Through High Wawe Forms, Proc. 7th China-Japan Semin. (Fukuoka 2013), volume 11 of Number Theory and Appl., pp. 95–144, New Jersey, London, Singapore, Beijing, Shanghai, Hong Kong, Taipei, Chennai, 2015. World Scientific Publishing Co. https://doi.org/10.48550/arXiv.1407.4216"> https://doi.org/10.48550/arXiv.1407.4216
S.N. Mergelyan. Uniform approximations to functions of complex variable. Usp. Mat. Nauk., 7(2):31–122, 1952 (in Russian).
H. Mishou. Functional distribution for a collection of Lerch zeta-functions. J. Math. Soc. Japan, 66(4):1105–1126, 2014. https://doi.org/10.2969/jmsj/06641105"> https://doi.org/10.2969/jmsj/06641105
H.L. Montgomery. Topics in Multiplicative Number Theory. Lecture Notes Math. Vol. 227, Springer-Verlag, Berlin, 1971. https://doi.org/10.1007/BFb0060851"> https://doi.org/10.1007/BFb0060851
T. Nakamura. Applications of inversion formulas to the joint tuniversality of Lerch zeta functions. J. Number Theory, 123(1):1–9, 2007. https://doi.org/10.1016/j.jnt.2006.05.012"> https://doi.org/10.1016/j.jnt.2006.05.012
T. Nakamura. The existence and the non-existence of joint t-universality for Lerch zeta-functions. J. Number Theory, 125(2):424–441, 2007. https://doi.org/10.1016/j.jnt.2006.12.008"> https://doi.org/10.1016/j.jnt.2006.12.008
T. Nakamura. The universality for linear combinations of Lerch zeta functions and the Tornheim–Hurwitz type of double zeta functions. Monatsh. Math., 162(2):167–178, 2011. https://doi.org/10.1007/s00605-009-0164-5"> https://doi.org/10.1007/s00605-009-0164-5
A. Reich. Werteverteilung von Zetafunktionen. Arch. Math., 45:440–451, 1980.
A. Rimkevičienė and D. Šiaučiūnas. On discrete approximation of analytic functions by shifts of the Lerch zeta-function. Mathematics, 10(24):4650, 2022. https://doi.org/10.3390/math10244650"> https://doi.org/10.3390/math10244650
J. Steuding. Value-Distribution of L-Functions. Lecture Notes Math. vol. 1877, Springer, Berlin, Heidelberg, 2007. https://doi.org/10.1007/978-3-540-44822-8"> https://doi.org/10.1007/978-3-540-44822-8
S.M. Voronin. Theorem on the “universality” of the Riemann zeta-function. Izv. Akad. Nauk SSSR, Ser. Matem., 39:475–486, 1975 (in Russian).
View article in other formats
CrossMark check
Published
Issue
Section
Copyright
Copyright (c) 2024 The Author(s). Published by Vilnius Gediminas Technical University.
License
This work is licensed under a Creative Commons Attribution 4.0 International License.