Curvature based characterization of radial basis functions: application to interpolation
DOI: https://doi.org/10.3846/mma.2023.16897Abstract
Choosing the scale or shape parameter of radial basis functions (RBFs) is a well-documented but still an open problem in kernel-based methods. It is common to tune it according to the applications, and it plays a crucial role both for the accuracy and stability of the method. In this paper, we first devise a direct relation between the shape parameter of RBFs and their curvature at each point. This leads to characterizing RBFs to scalable and unscalable ones. We prove that all scalable RBFs lie in the 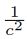
Keywords:
radial basis functions, shape parameter, curvature, interpolationHow to Cite
Share
License
Copyright (c) 2023 The Author(s). Published by Vilnius Gediminas Technical University.

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
M. Bozzini, L. Lenarduzzi, M. Rossini and R. Schaback. Interpolation with variably scaled kernels. IMA Journal of Numerical Analysis, 35(1):199–219, 2015. https://doi.org/10.1093/imanum/drt071"> https://doi.org/10.1093/imanum/drt071
M. Bozzini, L. Lenarduzzi and R. Schaback. Adaptive interpolation by scaled multiquadrics. Advances in Computational Mathematics, 16(4):375–387, 2002. https://doi.org/10.1023/A:1014584220418"> https://doi.org/10.1023/A:1014584220418
G.E. Fasshauer. Meshfree approximation methods with MATLAB. World Scientific, 2007.
G.E. Fasshauer and M.J. McCourt. Kernel-based approximation methods using MATLAB. World Scientific Publishing Company, 2015. https://doi.org/10.1142/9335"> https://doi.org/10.1142/9335
B. Fornberg and J. Zuev. The Runge phenomenon and spatially variable shape parameters in RBF interpolation. Computers & Mathematics with Applications, 54(3):379–398, 2007. https://doi.org/10.1016/j.camwa.2007.01.028"> https://doi.org/10.1016/j.camwa.2007.01.028
B. Fornberg and J. Zuev. The Runge phenomenon and spatially variable shape parameters in RBF interpolation. Computers & Mathematics with Applications, 54(3):379–398, 2007. https://doi.org/10.1016/j.camwa.2007.01.028"> https://doi.org/10.1016/j.camwa.2007.01.028
M. Heidari, M. Mohammadi and S. De Marchi. A shape preserving quasiinterpolation operator based on a new transcendental RBF. Dolomites Research Notes on Approximation, 14(1):56–73, 2021. https://doi.org/10.14658/pupj-drna-2021-1-6"> https://doi.org/10.14658/pupj-drna-2021-1-6
E.J. Kansa. Multiquadrics-A scattered data approximation scheme with applications to computational fluid-dynamics-II solutions to parabolic, hyperbolic and elliptic partial differential equations. Computers & Mathematics with applications, 19(8-9):147–161, 1990. https://doi.org/0.1016/0898-1221(90)90271-K"> https://doi.org/0.1016/0898-1221(90)90271-K
E.J. Kansa and R.E. Carlson. Improved accuracy of multiquadric interpolation using variable shape parameters. Computers & Mathematics with Applications, 24(12):99–120, 1992. https://doi.org/10.1016/0898-1221(92)90174-G"> https://doi.org/10.1016/0898-1221(92)90174-G
L. Ling. A univariate quasi-multiquadric interpolation with better smoothness. Computers & Mathematics with Applications, 48(5):897–912, 2004. https://doi.org/10.1016/j.camwa.2003.05.014"> https://doi.org/10.1016/j.camwa.2003.05.014
B. Óneill. Chapter 7 - Riemannian geometry. In Elementary Differential Geometry (Second Edition), pp. 321–387. Academic Press, Boston, 2006. https://doi.org/10.1016/B978-0-12-088735-4.50011-0"> https://doi.org/10.1016/B978-0-12-088735-4.50011-0
R.S. Palais. A modern course on curves and surfaces. Virtual Math Museum, 2011. Available from Internet: https://virtualmathmuseum.org/Surface/a/bk/curves_surfaces_palais.pdf"> https://virtualmathmuseum.org/Surface/a/bk/curves_surfaces_palais.pdf
H. Ratliff. Cartesian formulas for curvature, circumradius, and circumcenter for any three two-dimensional points. Zenodo, 2019. https://doi.org/10.5281/zenodo.2556424"> https://doi.org/10.5281/zenodo.2556424
M. Rossini. Interpolating functions with gradient discontinuities via variably scaled kernels. Dolomites Research Notes on Approximation, 11(2):3–14, 2018. https://doi.org/10.14658/pupj-drna-2018-2-2"> https://doi.org/10.14658/pupj-drna-2018-2-2
S.A. Sarra and D. Sturgill. A random variable shape parameter strategy for radial basis function approximation methods. Engineering Analysis with Boundary Elements, 33(11):1239–1245, 2009. https://doi.org/10.1016/j.enganabound.2009.07.003"> https://doi.org/10.1016/j.enganabound.2009.07.003
R. Schaback. Error estimates and condition numbers for radial basis function interpolation. Advances in Computational Mathematics, 3(3):251–264, 1995. https://doi.org/10.1007/BF02432002"> https://doi.org/10.1007/BF02432002
A.K. Singh and B.S. Bhadauria. Finite difference formulae for unequal subintervals using Lagrange’s interpolation formula. International Journal of Mathematical Analysis, 3(17):815–827, 2009.
View article in other formats
Published
Issue
Section
Copyright
Copyright (c) 2023 The Author(s). Published by Vilnius Gediminas Technical University.
License

This work is licensed under a Creative Commons Attribution 4.0 International License.

