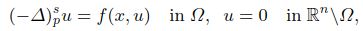Existence results for fractional p-Laplacian systems via young measures
DOI: https://doi.org/10.3846/mma.2022.14452Abstract
In this paper, we show the existence result of the following fractional p-Laplacian system
for a given datum f. The existence of weak solutions is obtained by using the theory of Young measures.
Keywords:
fractional p-Laplacian system, weak solution, Galerkin method, Young measureHow to Cite
Share
License
Copyright (c) 2022 The Author(s). Published by Vilnius Gediminas Technical University.

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
L. Ambrosio, G. De Philippis and L. Martinazzi. Gamma-convergence of nonlocal perimeter functionals. Manuscripta Mathematica, 134(3-4):377–403, 2011. https://doi.org/10.1007/s00229-010-0399-4"> https://doi.org/10.1007/s00229-010-0399-4
E. Azroul and F. Balaadich. Weak solutions for generalized p-Laplacian systems via Young measures. Moroccan Journal of Pure and Applied Analysis, 4(2):77– 84, 2018. https://doi.org/10.1515/mjpaa-2018-0008"> https://doi.org/10.1515/mjpaa-2018-0008
E. Azroul and F. Balaadich. Existence of solutions for a class of Kirchhoff-type equation via Young measures. Numerical Functional Analysis and Optimization, 42(4):460–473, 2021. https://doi.org/10.1080/01630563.2021.1885044"> https://doi.org/10.1080/01630563.2021.1885044
E. Azroul and F. Balaadich. On strongly quasilinear elliptic systems with weak monotonicity. Journal of Applied Analysis, 27(1):153–162, 2021. https://doi.org/10.1515/jaa-2020-2041"> https://doi.org/10.1515/jaa-2020-2041
E. Azroul and F. Balaadich. A weak solution to quasilinear elliptic problems with perturbed gradient. Rendiconti del Circolo Matematico di Palermo, II, 70(1):151–166, 2021. https://doi.org/10.1007/s12215-020-00488-4"> https://doi.org/10.1007/s12215-020-00488-4
F. Balaadich and E. Azroul. Quasilinear elliptic systems in perturbed form. International Journal of Nonlinear Analysis and Applications, 10(2):255–266, 2019. https://doi.org/10.22075/ijnaa.2019.19034.2050"> https://doi.org/10.22075/ijnaa.2019.19034.2050
F. Balaadich and E. Azroul. On a class of quasilinear elliptic systems. Acta Scientiarum Mathematicarum, 87(1–2):141–152, 2021. https://doi.org/10.14232/actasm-020-910-z"> https://doi.org/10.14232/actasm-020-910-z
F. Balaadich and E. Azroul. Elliptic systems of p-Laplacian type. Tamkang Journal of Mathematics, 53(1):11–21, 2022. https://doi.org/10.5556/j.tkjm.53.2022.3296"> https://doi.org/10.5556/j.tkjm.53.2022.3296
J.M. Ball. A version of the fundamental theorem for Young measures. In PDEs and continuum models of phase transitions, volume 344, pp. 207–215. Springer, Springer, Berlin, Heidelberg, 1989. https://doi.org/10.1007/BFb0024945"> https://doi.org/10.1007/BFb0024945
B. Barrios, E. Colorado, A. De Pablo and U. Sa´nchez. On some critical problems for the fractional Laplacian operator. Journal of Differential Equations, 252(11):6133–6162, 2012. https://doi.org/10.1016/j.jde.2012.02.023"> https://doi.org/10.1016/j.jde.2012.02.023
G.M. Bisci. Fractional equations with bounded primitive. Applied Mathematics Letters, 27:53–58, 2014. https://doi.org/10.1016/j.aml.2013.07.011"> https://doi.org/10.1016/j.aml.2013.07.011
G.M. Bisci and D. Repovš. Higher nonlocal problems with bounded potential. Journal of Mathematical Analysis and Applications, 420(1):167–176, 2014. https://doi.org/10.1016/j.jmaa.2014.05.073"> https://doi.org/10.1016/j.jmaa.2014.05.073
L. Caffarelli, J.-M. Roquejoffre and O. Savin. Nonlocal minimal surfaces. Communications on Pure and Applied Mathematic, 63(9):1111–1144, 2010. https://doi.org/10.1002/cpa.20331"> https://doi.org/10.1002/cpa.20331
E. Di Nezza, G. Palatucci and E. Valdinoci. Hitchhiker’s guide to the fractional Sobolev spaces. Bulletin des sciences Math´ematiques, 136(5):521–573, 2012. https://doi.org/10.1016/j.bulsci.2011.12.004"> https://doi.org/10.1016/j.bulsci.2011.12.004
L.C. Evans. Weak convergence methods for nonlinear partial differential equations, volume 74. American Mathematical Society, 1990. https://doi.org/10.1090/cbms/074"> https://doi.org/10.1090/cbms/074
A. Fiscella, R. Servadei and E. Valdinoci. Density properties for fractional Sobolev spaces. Annales AcademiæScientiarum FennicæMathematica, 40(1):235–253, 2015. https://doi.org/10.5186/aasfm.2015.4009"> https://doi.org/10.5186/aasfm.2015.4009
N. Hungerbühler. A refinement of Balls theorem on Young measures. New York Journal of Mathematics, 3:48–53, 1997.
A. Iannizzotto and M. Squassina. 1/2-Laplacian problems with exponential nonlinearity. Journal of Mathematical Analysis and Applications, 414(1):372–385, 2014. https://doi.org/10.1016/j.jmaa.2013.12.059"> https://doi.org/10.1016/j.jmaa.2013.12.059
F. Jiao and Y. Zhou. Existence of solutions for a class of fractional boundary value problems via critical point theory. Computers & Mathematics with Applications, 62(3):1181–1199, 2011. https://doi.org/10.1016/j.camwa.2011.03.086"> https://doi.org/10.1016/j.camwa.2011.03.086 Special Issue on Advances in Fractional Differential Equations II.
A.A. Kilbas, H.M. Srivastava and J.J. Trujillo. Theory and applications of fractional differential equations, volume 204. Elsevier, 2006.
J.-L. Lions. Quelques méthodes de résolution de problemes aux limites non linéaires. Études mathématiques, 1969.
H. Qiu and M. Xiang. Existence of solutions for fractional p-Laplacian problems via Leray-Schauders nonlinear alternative. Boundary Value Problems, 83:1–8, 2016. https://doi.org/10.1186/s13661-016-0593-8"> https://doi.org/10.1186/s13661-016-0593-8
W. Rudin. Real and complex analysis. McGraw-Hill Book Company, New York, NY, 1966.
R. Servadei and E. Valdinoci. Mountain Pass solutions for non-local elliptic operators. Journal of Mathematical Analysis and Applications, 389(2):887–898, 2012. https://doi.org/10.1016/j.jmaa.2011.12.032"> https://doi.org/10.1016/j.jmaa.2011.12.032
K. Teng. Two nontrivial solutions for hemivariational inequalities driven by nonlocal elliptic operators. Nonlinear Analysis: Real World Applications, 14(1):867– 874, 2013. https://doi.org/10.1016/j.nonrwa.2012.08.008"> https://doi.org/10.1016/j.nonrwa.2012.08.008
M. Xiang, B. Zhang and M. Ferrara. Existence of solutions for Kirchhoff type problem involving the non-local fractional p-Laplacian. Journal of Mathematical Analysis and Applications, 424(2):1021–1041, 2015. https://doi.org/10.1016/j.jmaa.2014.11.055"> https://doi.org/10.1016/j.jmaa.2014.11.055
View article in other formats
Published
Issue
Section
Copyright
Copyright (c) 2022 The Author(s). Published by Vilnius Gediminas Technical University.
License

This work is licensed under a Creative Commons Attribution 4.0 International License.